Why don't glasses flow ? JP Bouchaud SPEC/CEA Saclay   & Science & Finance/CFM Paris More detailed discussion- pdf

Glasses are liquids that do not flow. Glasses look like liquids (atoms are in random, dense configurations), but behave like solids. More precisely, the time they need to flow rises extremely rapidly when the temperature is reduced, and soon exceeds the age of cathedrals (or of the universe, for that matter). Spin-glasses are, similarly, disordered magnets that remain frozen in random spin configurations, with no apparent order. Both type of systems reveal interesting properties: they age (their properties depend on the time they spent in the glassy state), and can memorize their history and simultaneously rejuvenate when the temperature is changed. A very important experimental observation is that the viscosity of glasses (a dynamical property) is highly correlated with its entropy, i.e., the number of microscopic configurations in which the glass can get stuck. The smaller this number, the larger the viscosity. The striking observation that makes the `problem of glasses' interesting is that very many, totally different materials, exhibit the same properties, pointing to the existence of a somewhat universal mechanism: glassy dynamics is physics more than chemistry.

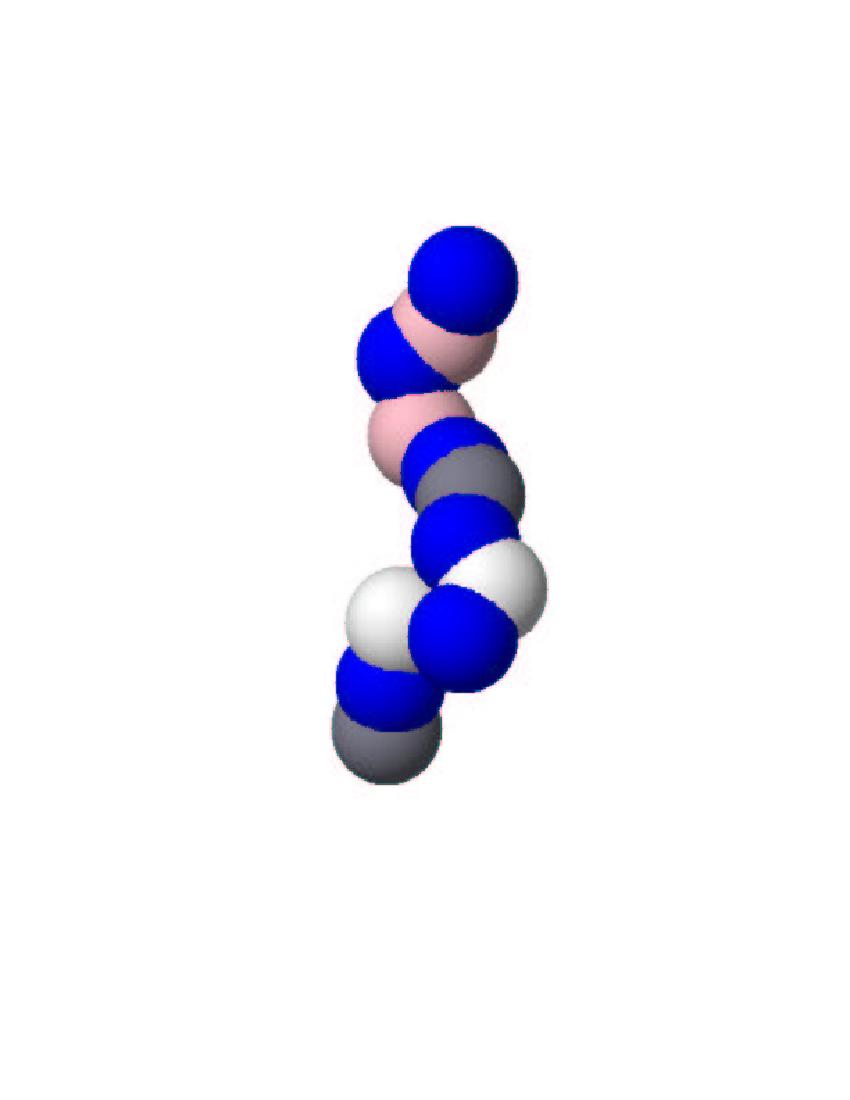
Is there a divergent length scale in glasses? One important  idea is that of ``cooperatively rearranging regions'' of increasing length. The dynamics becomes sluggish because larger and larger regions of the material have to move simultaneously to allow for a substantial motion of individual particles. Although this idea seems most reasonable, its reality has remained elusive until recently: the difficulty is that, contrarily to better understood systems where this length corresponds to the size over which the system has ordered (for example, as a crystal), glasses do not `order' in any obvious way. This cooperative length is purely dynamical and hence more more difficult to measure. A recent idea is that the elementary cooperative motion in glassy materials takes the form of strings (see figure). Interestingly, this concept may be also relevant for the description of other ``jammed'' systems, such as dense granular assemblies that flow in a very jerky way. If this cooperative length really exists, how large can it grow in real materials? Is it because this length can become large that all glassy materials behave in the same way, because microscopic details become irrelevant?

Glasses are fragile! A remarkable effect predicted in spin-glasses is their extreme fragility to tiny perturbations (such as temperature changes), that can induce large rearragements in the equilibrium configurations. Such a fragility was also appears in other contexts (pinned vortex lines, dislocations, domain walls; force chains in granular materials). Does this `temperature chaos' effect also extends to regular glasses and allows one to understand rejuvenation in these materials?

Glasses in the wider perspective From a wider perspective, one can ask how much glassy systems, with their profusion of quasi-equilibrium states and complex dynamics, can be used as metaphors in other contexts. Combinatorial optimization is a already a well studied one. Applications in economics/finance/game theory, where equilibrium is of ten assumed but may never be reached, is a fascinating prospect.