Frontiers of Condensed Matter: report

Frontiers in Correlated Matter:

Physicists meet to discuss the intellectual challenges of complex matter.

Piers Coleman and Leo Kadanoff

Main
Soft Matter

"Quantum Matter"

Condensed matter physics is generally divided in "hard" and "soft" condensed matter physics. "Hard" matter refers
to matter governed by atomic forces and quantum mechanics . Hard matter is generally not biological, and involves crystals, glasses, metals, semiconductors and oxides. "Soft" matter refers to the myriad varieties of matter that form on the macroscopic scale, often from biological, or organic molecules. Here the physics, though collective,
does not involve quantum mechanics, and the materials of interest are literally "softer".

Probing new phases of matter:

the fourth phase (Seamus Davis)
magnetic resonance imaging (Henri Alloul)
detecting broken symmetry (Laura Greene)

phase coherence and two dimensional metals (Myriam Sarachik)

Quantum phase transitions

a playground for discovering new quantum phases (Gil Lonzarich)
Black hole in the material phase diagram Zachary Fisk)
Quantum criticality and superconductivity (Frank Steglich)
Dark Law and emergence (Robert Laughlin)

Computing quantum matter

Computations on interacting quantum matter (Doug Scalapino)
Dynamical Mean Field Theory (Gabriel Kotliar)
Density Functional Theory (Marin Cohen)

Quest for Strange Metals

Strange metals and High Temperature Superconductivity (Phil Anderson)
Quantum Mayonnaise (Joerg Schmalian)

Probing new phases of matter.

One of the recurring themes here concerned the discovery of new phases of matter. As one tunes matter close to instability, it undergoes phase transitions into new electronic, or structural configurations, often with radically new properties. Detecting these changes in matter requires innovative new kinds of instruments and experimental methods. Four of the experimentalists at the meeting, Henri Alloul, Seamus Davis, Laura Greene and Myriam Sarachik described their experimental work that seeks to detect and characterize new phases of matter.

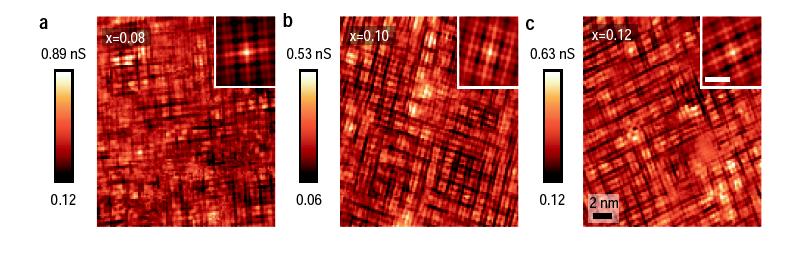
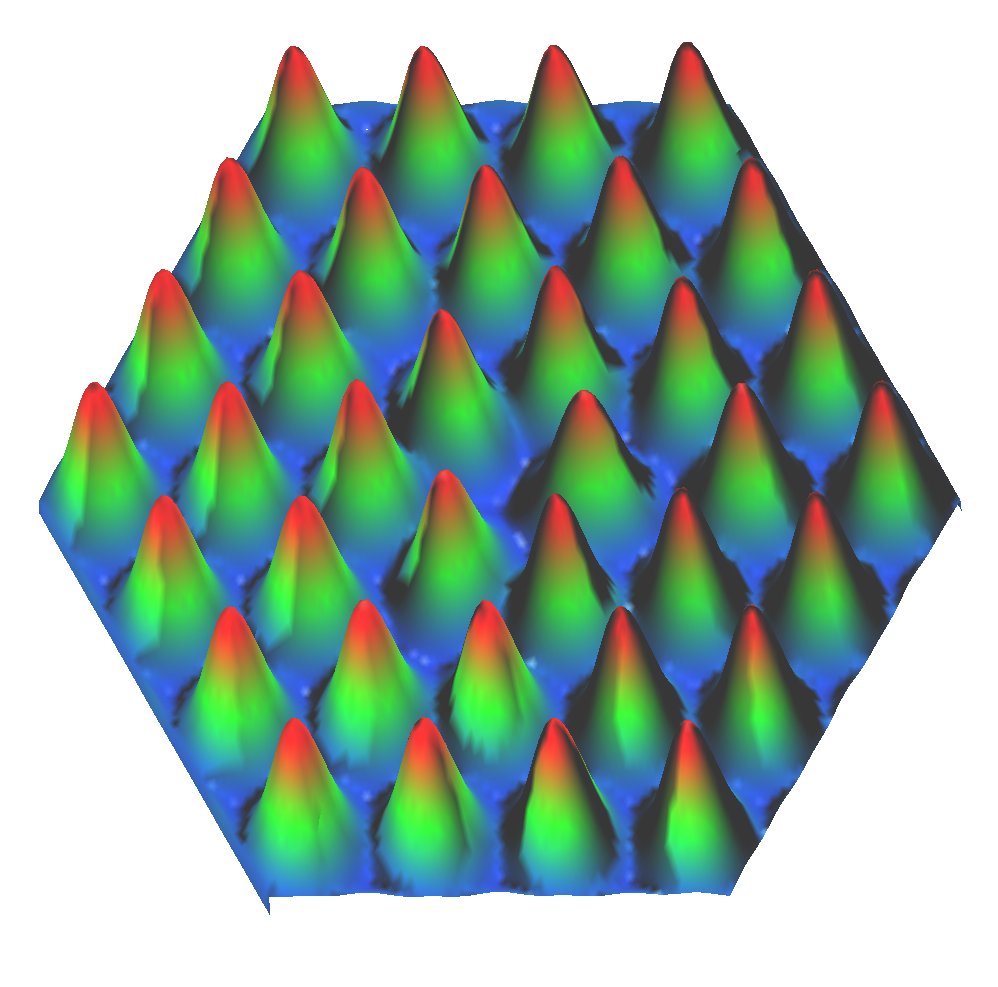
One approach, is to try to actually probe matter on the atomic scale. Henri Alloul and Seamus Davis described two new approaches to this problem.

The "fourth phase":

Seamus Davis

Seamus Davis' group has developed a new type of quantum microscope that can image electon matter on the atomic scale. An atomically sharp tip is manipulated atomically close to the surface of the material. When a voltage is applied to the tip, electrons quantum mechanically tunnel through the vacuum between the tip into the electron fluid inside the material. By measuring the tunneling current of electrons into the sample as a function of the voltage applied to the tip, one is able one is able to probe the energy distribution of the electrons. Scanning tunneling microscopes contain sophisticated piezo-electric feedback techniques that enable the tip to be held in one place, with sub-atomic precision. By slowly moving the tip across the surface, one can follow how the electron energy distribution depends on position, and this provides detailed information about the electron waves, and quantum matter that they are part of.

Seamus described how they have been able to examine a new phase of matter in high temperature superconductors.

In their raw state, these materials are insulators - but when charge is chemically injected into them, they transform from insulator to high temperature superconductor. Sandwiched between the two phases, is a mysterious state of matter, "the pseudo-gap phase" - where the electrons appear to develop some of the correlations of a superconductors without developing full blown superconductivity. Seamus calls this "the fourth phase", and its understanding may hold part of the key towards solving the mystery of high temperature superconductivity.

"Chequer board" structure observed in the under-doped cuprate superconductor, Calcium Copper Oxy-Chloride

Davis' group set out to image this fourth phase. This depended on the synthesis of a new cuprate material, a Copper Oxy-Chloride, which was carried out by Takagi's group at the ISSP, Tokyo. Copper Oxy Chlorid forms an ordered crystal at just the right doping to form the "fourth phase". Remarkably, this new phase, displays an electron energy distribution that is quite similar to the bulk superconductor - in particular - there is V -shaped gap in the spectrum. However- when they look carefully to see how this gap depends on location, they discovered a "chequer board" modulation of the electron energy spectrum, where each square in the structure is four unit cells in length.

Davis described how the data is consistent with the formation of an electronic (as opposed to an atomic) crystal. He speculated that this state might be a kind of ``supersolid'', (see figure) a crystal of electron pairs that simultaneously possesses the zero-resistance properties of a superconductor.

Up

Magnetic Resonance Imaging of Quantum Matter:

Henri Alloul

Henri Alloul of Orsay, France, showed how the same magnetic resonance imaging techniques used in medical devices can be also be used to probe deep inside quantum matter. The electron waves inside quantum matter carry tiny magnetic moments, or spin. As these spins pass by the atomic nucleii within the matter, they jiggle the spins of the nucleii, and this jiggling can be used to probe the local magnetic fluctuations inside the quantum matter.

Henri gave several examples of how magnetic resonance imaging had ellucidated new types of electron correlation in matter. One of the novel materials they've examined is a new state of carbon - the so-called "fullerene" material, in which carbon atoms combine in spheres to form tiny geodesic spheres, each containing sixty atoms or "C-60". When crystals of fullerene are combined with alkali atoms such as sodium or cesium, they develop superconductivity. Alloul's group was surprised when they measured the NMR spectrum of $CsC_{60}$, finding that when two electrons are transfered from the cerium atoms, to the buckyballs, they are forced to enter the buckyball with their spins in an antiparallel configuration, or "singlet". Remarkably, the buckyball distorts as the electrons enter. This distortion is thought to be closely related to be the mechanism by which electrons pair in C-60 to develop moderately high temperature superconductivity.

Alloul showed how magnetic resonance imaging can be used to image the magnetic ripples that eminate from an impurity that has been lodged inside a crystal. Normally, these ripples don't develop if the impurity is not magnetic- but remarkably inside cuprate superconductors, these ripples develop even when the impurity is non-magnetic - as if one generated ripples on a pond without throwing the stone!

Detecting broken Symmetry: Laura Greene

In her talk, Laura Greene, from University of Illinois, Urbana Champaign, described how broken symmetry drives matter to develop new properties Broken symmetry is a cosmic principle which governs matter in solids, superconductors, magnets, and it is even responsible for the weak nuclear force that governs the production of light from the sun. For example, by breaking the translational symmetry of the liquid, a crystal develops its sheer rigidity. A still more subtle symmetries is gauge symmetry, a symmetry possessed jointly by charged particles and the electromagnetic field. Laura described how, broken gauge symmetry is responsible for the laser and superconductivity.

Laura described the difference between the broken symmetry in conventional, superconductors, and the extra broken symmetry found in the group of "anisotropic" superconductors that includes high temperature superconductivity. Superconductivity is produced by the formation of bound "Cooper pairs" of electrons, and it is the symmetry of the Cooper pair wavefunction electrons that delineates conventional, and unconventional superconductors. In conventional superconductors the Cooper pair wavefunction has "s-symmetry", with a single sign, which means that the properties of electrons do not depend on the direction in which they are moving. In anisotropic superconductors, the Cooper pair wavefunction changes sign - forming, for example a d-wave which looks like a kind of clover leaf. This means that the properties of electrons depend on the direction in which they are moving. Some believe that the high transition temperature of cuprate superconductors is linked to the additional broken symmetry of their Cooper pairs. But how does one detect broken symmetry?

Greene showed ways in which the symmetry of paired electrons in superconductors can be probed using the methods of electron tunneling. Unlike conventional superconductivity, which is largely insensitive to the surface of the material, anisotropic superconductivity is suppressed near the surface. This gives rise to new kinds of surface bound-state, which appear as peaks in the electron tunneling spectra. Using these methods, Greene's group have been able to confirm the "d-wave" symmetry of cuprate superconductors, and in some cases, show that the superconductivity at the surface breaks a new kind of symmetry - time reversal symmetry. Her group is currently engaged in the development of new kinds of tunnel junction that will be used to probe the broken symmetry of superconductors of the future. Phase coherence and 2D metals.

General introductory article "High Temperature Superconductors: Playgrounds for broken symmetries"
Up

Phase Coherence and 2-dimensional metals:

Myriam Sarachik

One vital aspect of quantum matter is "phase coherence". Lasers and superconductors are examples of phase coherent matter. Myriam Syrachik of City College, New York, pointed out that phase coherence has a much wider significance. For example, if we are to develop the quantum computer of the future, we need to find ways of preserving and protecting phase coherence from the outside world.

Sarachik talked about efforts to understand the phase coherence of electrons in two dimensional metals that form inside certain kinds of semi-conductor called "Silicon Mosfets". These two dimensional metals defy our understanding about the forces between electrons affect their quantum mechanical wave propagation. For many years, it was believed impossible to have a metallic state in two dimensions. In pioneering work by a group now known as the "gang of four", it was shown that when electrons do not interact, there can not be a metal in two dimensions. In the presence of disorder, electrons back-scatter - and in this back-scattering process, electrons preserve their phase memory. The time reversed paths that contribute to back-scattering constructively interfere with one-another ... and this constructive interference builds up to localize electrons. It was also shown that when electrons interact weakly, they are still localized.


	Electrons interfere along time-reversed paths causes localization.

At the end of the cold war, measurements on ultra- high mobility silicon mosfets that came from the Soviet Union astounded scientists. Silicon mosfets are a particular type of transistor in which one can create a perfectly flat two dimensional electron gas. In these new new mosfets, experimentalists could form very low density electron gases, where the interaction energy of the electrons becomes much larger than their kinetic energy. The fascinating discovery, was that as the carrier density was increased inside the Mosfet, the electron gas transformed itself from an insulator - which was expected - into a metal - a complete surprise!

There are many new ideas about the way electrons might correlate themselves to produce this new physics, some involving magnetism, some involving the formation of an electron crystal first proposed by Wigner more than half a century ago. This is a wonderful example of how new technology leads to new insights about matter.

Two dimensional Wigner Crystal

Sarachik ended her discussion by talking about some more general aspects of quantum coherence, pointing out that as the size of transistors drops down towards the atomic scale - a phenomenon known as Moore's law- we are having to cope more and more with the issue of quantum mechanical coherence of electrons. One of the dreams is that we may be able to turn quantum coherence to our advantage in the "Quantum Computer".

Up

Quantum Phase Transitions:

Another major topic was quantum phase transitions, which occur when a finite temperature phase transition is suppressed to zero.

"A playground for discovery of new quantum phases": Gilbert Lonzarich

Gilbert Lonzarich of Cambridge University pointed out that quantum phase transitions are an important route towards discovering new quantum states of matter. A quantum phase transition is a new kind of melting transition. Conventional melting occurs because random thermal jiggling of atoms breaks up a cystal structure. Quantum phase transitions occur at absolute zero - they are not driven by thermal motion, but by the jiggling "zero-point motion" of the electrons associated with the Heisenbergs uncertainty principle. Lonzarich cited some of the remarkable discoveries that have resulted from careful examination of such quantum melting transitions, including the co-existence of p-wave superconductivity and ferromagnetism in Uranium-Germanium-2, and the appearance of a strange new paramagnetic metal in Manganese Silicon under pressure, in which the resistivity depends as T^3/2, quite unlike conventional metals.

Up

"A Black hole in the material phase diagram.": Zachary Fisk

Zachary Fisk of UC Davis likened Quantum Phase transitions to a kind of "Black Hole singularity" in the material phase diagram, because of their profound abilities to transform the properties of the across a wide range of temperatures near to the quantum phase transition. Gilbert Lonzarich of Cambridge and Frank Steglich from the Max Planck Institute of Chemical Physics in Dresden showed many examples of how magnetic quantum phase transitions transform materials, giving rise to new kinds of strange metal and often inducing superconductivity. This is a very exciting area whose understanding may herald a new fusion of ideas from statistical mechanics and correlated electron physics.

"Quantum Critical Point: singularity
in the material phase diagram.

Fisk described a class of f-electron f-electron material that has proven invaluable in the study of quantum phase transitions. f-electron materials, he said, contain rare earth or actinide atoms such as such as Cerium, Ytterbium, or Uranium, in which the electronically active f- electrons are localized to form tiny magnetic tops, so small that one needs to use the laws of quantum mechanics to describe their motion. Frank Steglich described how, as one cools an f-electron material, the mobile electrons progressively screen the tiny quantum tops, and as they do so, a new fluid of "heavy electrons" emerges. Heavy electron metals have proven to be a huge playground for studying correlated electrons.

Up

Quantum Criticality and Superconductivity:

Frank Steglich

Color coded plot of the field induced phase diagram of a heavy fermion metal. As the material is tuned with magnetic field, it passes through a quantum critical point.

Steglich described how many labs worldwide, have been able to destablize heavy electron metals, causing them to transform into an antiferromagnetic state, in which their spins are locked together in a staggered arrangement. The point of transition is the Quantum Critical point. Steglich argued that there are two types of such transition - one - a spin density wave transition, in which a density wave of oscillating magnetization condenses within the heavy electron fluid - a second - called a local quantum phase transition, in which the magnetism appears to develop through a loss of screening of the magnetic ions. This second class of transition appears to fit into Zachary Fisk's notion of a "Black hole of magnetism". Frank showed a remarkable set of data that suggest that at this second class of phase transition, the heavy electrons seem to actually disintegrate into their spin and charge components.

Up

"Dark Law" and emergence:

Bob Laughlin

"Biologists invented the concept of emergence - I learnt it - emergence, through Phil (Anderson) and (Stuart) Kauffmann", Laughlin remarked, "but our field is the one that actually proved that emergence exists".

Bob Laughlin used the topic of quantum phase transitions to illustrate some provocative ideas on the meaning of emergence. Emergence, he described, is one of the great contributions of condensed matter physics to science.

Laughlin argues that in condensed matter physics, we have discovered laws that were not anticipated from basic quantum mechanics. The discovery of these laws didn't happen deductively, starting with the Schrodinger equation, but rather, through the study of the organization of matter. "My own feeling", he stated, "is that the organization of the matter makes the mathematics work, not the other way around. Matter has phase coherence - these relations become increasingly exact, and I have mastery over the mathematics. In cases where that doesn't work - you're in trouble."

Laughlin argued that the failure of the field of condensed matter physics to make progress understanding certain problems, such as the phase diagram of high temperature superconductors - is because near quantum critical point, matter is "phase conflicted", so that the tiniest perturbation will push the system from one state to another. He provocatively refered to this tendency as an example of something he called "Dark Law".

Laughlin's "Dark Law" is in some ways, the antithesis of conventional emergent behavior, where, even if you make a mistake in your calculations, the phenomenon is so robust, that will still deduce the key properties. These are, he argues, examples of "good laws". By contrast, regions of quantum criticaliy are so sensitive, that nature actual prevents the theoretical physicist from deducing the laws that govern it, and on the experimental side, experiments become irreproduceable.

Laughlin's talk encouraged much debate. Michael Cates (Edinburgh) and Steve Berry of the University of Chicago suggested that Laughlin was asking the the wrong questions - and that when you change the question - there would be no more "Dark Law". Tom Rockwell - artist and museum exhibitor remarked that from the standpoint of the artist, the discovery that physics doesn't have ultimate control over the understanding of matter - was -quite frankly "a relief". Phil Anderson - one of the pioneers of the idea of emergence in condensed matter - remarked that he was much less pessimistic about science than Laughlin, and that despite big disagreements between scientists - experiments on the spectroscopy of high temperature superconductors had converged to a consensus. He felt that the main problem was sociological - that partly because of the pressure of funding agencies, we have developed an environment where it has become almost impossible to admit error. Dark law, in his opinion was a sociological, rather than a scientific issue.

Up

Computing quantum matter

One of the great challenges addressed by the quantum condensed matter community, concerns our ability to compute and model the properties of quantum matter using computers. Doug Scalapino, UC Santa Barbara, discussed the progress that has been made trying to deal with simple models, making no approximations about the interactions. There are no new high rise buildings, no new aircraft, and no new cars are built without today without the guide of numerical simulations, Scalapino pointed out. What about numerical simulations of quantum systems?

Three of the participants at the meeting, Marvin Cohen from UC Berkeley, Gabriel Kotliar from Rutgers University, New Jersey and Doug Scalapino offered contrasting perspectives on this great challenge. There are two competing desires in the community that we struggle to deal with. On the one hand, there is conciousness that the details of the real material are very important - that one needs to include the detailed symmetries of the orbitals and crystal structure if one is to understand real materials. On the other hand, the inclusion of these details often compromises one's ability to include the effects of electron-electron interactions, and the collective behavior that they give rise to. How should one deal with these conflicting demands?
Up

Exact computations on interacting models:

Doug Scalapino

Scalapino's research is strongly motivated by the unsolved problem of high temperature superconductivity. There are tens of thousands of new theories about high temperature superconductivity - he mused - and the reason that we can talk about all of these models of high temperature superconductivity, is that we don't know with any qualitative precision, how even the simplest models of these systems behave. By providing a more qualitative idea of the physics of the simplest models of strongly correlated electrons, numerical methods can remove some of this uncertainty, he said. Looking further afield, he would like to answer questions such as, what limits Tc, and why does it rise to 160K in the Mercury based cuprate superconductors?

Scalapino acknowledged that numerical calculations are limited to small size systems - so one can't solve the complete problem - yet - one can obtain some interesting new insights. In the last decade or so - many new numerical methods have become available - fast, exact diagonalization or "Lanczos" methods which are limited to about 36 atoms - the "Density Matrix Renormalization Group" approach, which can examine infinitely long linear chains or ladders with a small number of legs - and lastly, Quantum Monte Carlo - where one can "go large", but in a restricted class of insulating spin problems where there is no sign problem.

While these methods have given a lot of new insight into the undoped cuprate problem, into two-leg ladder compounds and to certain classes of frustrated antiferromagnet - the doped two dimensional Hubbard model is at best, only partly understood from numerical work. One of the great barriers to progress using Monte Carlo techniques, is the presence of the "sign problem". In Monte Carlo, one computes a weight to each configuration. Quantum mechanical interference causes some of these configurations to have negative weight - and at present, the only approach that can be taken, is to drop these configurations. While this does still give the right answer - the larger the number of negative weight states that appear, the more inaccurate the computation - and this is exactly what happens in the doped Hubbard model. This surely represents one of the great challenges to the numerical community in the future.

Nevertheless, great advances have been made - one can for example show that there is a strong tendency towards superconductivity in the cuprates by studying ladder compounds - and here - numerics has shown that one has d-wave superconductivity , as seen in experiments. There are many new approaches being developed to try to address these limitations in the future, Scalapino argued. Some are trying to solve the fermion sign problem. Ideas from the field of quantum information are helping to design better density matrix renormalization group algorithms. On another front, there is the idea that one can use ultra-cold nuetral atoms in an optical lattice as a kind of analog quantum simulator.

Up

Dynamical Mean Field Theory:

Gabriel Kotliar

Gabi Kotliar of Rutgers University pointed out that a large variety of materials that have been discovered in the last two decades can not be understood interms of what is known as the "standard model of physics" - the idea that the excitations of the material can be divided up into electron quasiparticle excitations, weakly coupled to collective modes. As two examples of bad actor materials, Gabi Kotliar cited

- the oxide Lithium Vanadate, which (like the cuprate superconductors) exhibits a mysterious, large, linear and non-saturated resistivity, - the "Kondo insulator" Iron Silicide - a metal in which the interactions between the electrons cause it to become insulating at low temperatures, in which the lost optical conductivity at low frequencies is not recovered up to very high frequencies - effectively violating the venerable f-sum rule which states that the integrated optical response of a material is a conserved quantity.

Kotliar argued that we need a new way to think about these phenomena - and at the same time we need to find a method by which we can compute what is going on without over-simplifying important details of the material. He described a new approach called "Dynamical mean field theory"(DMFT) - which goes a part way towards achieving these goals. In DMFT, one regards quantum matter as a background medium in which the collective modes are non-interacting, into which one embeds the strongly correlated local quantum degrees of freedom - which might be individual atoms - or possibly, clusters of plaquettes of atoms. The interaction between the medium and the local degrees of freedom is taken into account exactly, and this is used to compute the modes of the medium, and the calculation is continued until one reaches an self-consistent description of the medium. In this way, one hopes to capture the physics of both the atomic, and the band limit of quantum matter.

This approach has been very successful in developing a description of the Mott-Hubbard gap which develops in strongly correlated electron insulators, and for these systems, one can see the optical weight shifting to high energies, as observed in experiment. Nowadays, the big push is to develop cluster DMFT, in which the active local quantum degree of freedom in the lattice is a plaquette.

Kotliar argued that these kind of approaches offer the same kind of promise for understanding, and predicting the properties of correlated materials, as the one-electron "density functional" approaches have been in weakly interacting materials.

Up

Density Functional Theory:

Marvin Cohen

Marvin Cohen, UC Berkeley, and currently President of the American physical society talked about the importance of defining the field of physics, and the vital role that condensed matter physics plays at the center of the discipline. Cohen argued that physics - as the study of matter and energy - lies at the core of the physical sciences, and that its success in the future will depend on its ability to maintain its links and breadth. He very much hoped that the emerging fields of nanophysics and biological- with their huge potential for discovery - will remain key elements of the physics community.

Marvin cited the great success of the fields of particle physics and cosmology - in unifying their effort to understand the cosmos at large and small, citing the "Quantum Universe Report" by Persis Drell as a marvellous example of how the two fields have drawn together. Part of the difficulty he said, in trying to unify condensed matter physics, is its sheer breadth. Condensed matter physics, he argued - is the part of physics that is most highly coupled to science and industry - and these connections, together with this diversity are part of its strength that need to be emphasized.

Putting on his hat as researcher, Marvin returned to the discussion of numerical approaches to correlated matter. Cohen has pioneered of the "one electron" approach to modelling real materials, in which one endeavors to find the best free-electron description, emphasizing the detail in the one-electron aspects of the description, while treating interactions in an average way as a so called "pseudo-potential".

Cohen emphasized the huge successes of this approach - in understanding the nature of the chemical bond - the structural, mechanical and vibrational properties of materials - the interactions between electrons and the lattice- and accurate descriptions of phonon-mediated superconductivity. There is a wide swath of material behavior, he argued that is due to the details of one-electron physics - joking - that those working on strongly correlated materials should "take a one-electron person out to lunch" to discover these successes. Turning to the future of these approaches - he cited multi-wall nanotubes, as a wonderful example of the progress that is being made. Here, there are cylinders within cylinders which can be moved in and out inside one-another - offering a unique chance to understand friction on the nanoscale.

There was much discussion with the audience about the power of computers to understand complex matter. Pierre Hohenberg of New York University, remarked noted that "the Dog did not bark", by which he meant that none of the speakers working on quantum matter had lamented "if only I had a computer that is a million times bigger." Indeed - he noted - real progress appears to be made by finding better algorithms: better methods of calculation. "It gives one pause", he said "about understanding biology by taking all the data and using computers. You hear it over and over - and its sobering to hear - that the dog did not bark. "

Marvin Cohen agreed with this view. He pointed out that in the one-electron effort - you'd be better off with the algorithms of today and a computer of the 70s versus the computers of today and the algorithms of the 70s. He ended his talk by reminding us of a quote by Einstein:

"The most valuable tool of the theoretical physicist is his wastebasket."

Up

Quest for Strange Metals

One of the other recurrant interests in correlated matter is the possibility of totally new kinds of metal. Phil Anderson from Princeton and Jeorg Schmalian from Ames lab discussed three different aspects of strange metals.

Up

Strange Metals and High Temperature Superconductors:

Phil Anderson

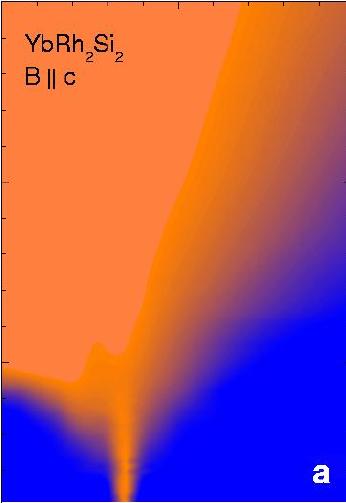
Phil Anderson began his talk by remarking on a number of interesting questions about correlated matter.

Anomalous superconductors - such as the actinide and rare-earth superconductors refered to by Frank Steglich and Gilbert Lonzarich - raise a number of fascinating unsolved questions. For example, these materials can occur in a state where the valence of the active ions is in a quantum mechanical state of fluctuation - mysteriously, such materials never show anomalous superconductivity. Why are there no "mixed valent" superconductors?

Anderson asked. Anderson also cited the recently discovered "Cobaltate Superconductors". The low energy electrons in conventional metals have certain allowed momenta that lie on a surface called the "Fermi surface". Normally, the volume of this surface determines the density of mobile electrons - but in the colbatates he reflected - it appears that the Fermi surface has the wrong volume: why?

As a final introductory topic, Phil mentioned quark-gluon plasmas, where it appears that the current experiments at the RHIC collider have revealed a new kind of quantum fluid. This appears to be a very interesting area for future theoretical discussion, he said.

Phil Anderson turned to the main focus of his discussion - the unsolved problem of "strange metals". He pointed out that conventional metals can be understood in terms of Landau's quasiparticle theory of metals. According to Landau's theory, even though electrons inside metals exert quite large Coulomb repulsive forces on each other, at low energies they become screened by the surrounding fluid, forming "quasiparticles", which carry the same charge and spin as electrons, but which interact weakly. Landau's theory is the standard model on which we base almost all of our understanding of conventional metals.

Phil Anderson argued that there is a large and important class of new materials for which this "standard model" fails, so that the interaction between the electrons remains large at low energies. Anderson argues that the normal state of the high temperature superconductors. Here Anderson went to some pains to draw the distinction between the underdoped, so called "pseudo-gap" phase of these superconductors, and the "optimally doped" versions which have the highest superconducting transition temperature. Anderson argued that the former category - the pseudo-gap materials can be understood as a liquid of spin-singlets in which the spins are combined into a wavefunction with d-symmetry. This he said, is well understood. At optimal doping however, the pseudo-gap phase does not develop - and the normal state is an unusual, or "strange metal".

According to these ideas, the wavefunction of the electronic fluid that forms in the strange metal is very different to a conventional metal, and contains "Jastrow" correlations that keep the electrons apart. Another important aspect of this metal, is that it is far easier to remove electrons to the metal, than to add them. This is called an "electron-hole" asymmetry, and it has important consequences for various electron spectroscopies of high temperature superconductors.

Quantum Mayonnaise:

Joerg Schmalian

Joerg Schmalian presented an alternative view of strange metals, motivated by the recent discoveries mentioned by Lonzarich, on the magnetic metal manganese silicide. When subjected to pressure, manganese silicide (MnSi) enters a strange metal phase, with an unusual temperature dependence of the resistivity. Joerg argued that this phase of matter could be understood using ideas borrowed from soft condensed matter - as a quantum version of jello. This material would at one and the same time show quantum properties and also jello's ability to remember its shape. Hence it would be a sort of quantum version of a glass. He offered the exciting idea that it's low temperature phase would be a superposition among quantum states, offering the possibility of studying such a partially coherent phase. This kind of phase might serve as one kind of model for phases of the entire observable universe.